TI Politala Matdis 1 C

Assalamualaikum Warohmatullohi Wabarokatuh...

Hello guys... 

Pada kesempatan kali ini saya akan sedikit mengulas materi Matematika Diskrit tentang "Fungsi".

Materi kali ini dapat kalian gunakan sebagai bahan referensi ataupun bahan literasi dalam belajar.

Ok deh, langsung aja kita bahas materinya.

Semoga bermanfaat yaa...

FUNGSI

A. Pengertian Fungsi

Fungsi adalah sebuah relasi binary dimana masing-masing anggota dalam himpunan A (domain) hanya mempunyai satu bayangan pada himpunan B (kodomain).

Notasi fungsi :

f : A →  B

dibaca f adalah fungsi dari A kedalam B atau f memetakan A kedalam B.

            Jika himpunan A = B, maka f : A →  A disebut operator atau transformasi pada A.

Contoh :

            Misalkan A = {Ms.Word, Word Pad, Ms.Excel, Lotus 123, Paint Shop Pro, Gimp}

                            B = {Pengolah kata, Pengolah data, Pengolah gambar}

            Misalkan f : A →  B

Himpunan A disebut ranah (domain) dari fungsi f.

Himpunan B disebut ko-ranah (kodomain) dari fungsi f.

               Pengolah kata adalah bayangan dari Ms.Word dan Word Pad, dinyatakan oleh :

f (Ms.Word) dan

f (Word Pad)

               Jangkauan (range) dari f adalah (Pengolah kata, pengolah data, dan pengolah gambar).

B. Macam-Macam Fungsi

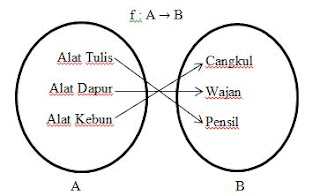
     1. Fungsi Injektif (satu-satu)

          Sebuah fungsi f : A →  B dikatakan fungsi satu-satu jika dan hanya jika setiap elemen pada himpunan B (kodomain) mempunyai pasangan hanya satu saja, dan walupun ada yang kosong.

Contoh :

A : {Alat Tulis, Alat Dapur, Alat Kebun}

B : {Cangkul, Wajan, Pensil, Flashdisk}

2. Fungsi Surjektif (Pada)

              Sebuah fungsi f : A →  B dikatakan fungsi pada, jika dan hanya jika setiap elemen himpunan B harus muncul sebagai bayangan sekurang-kurangnya satu elemen dari himpunan A dan boleh lebih dari satu bayangan.

     Contoh :

     A : Himpunan Software Aplikasi

     B : Himpunan Sistem Operasi

     3. Fungsi Bijektif (Satu-Satu Pada / Korespondensi Satu-Satu)

          Suatu fungsi f : A →  B dikatakan fungsi konstan jika dan hanya jika semua elemen himpunan B mempunyai pasangan dan hanya boleh 1 pasang dari seluruh elemen himpunan A.

Contoh :

A : {Sayuran, Buah-buahan, Hewan-hewan}

B : {Ayam, Kangkung, Mangga}

     4. Fungsi Invers

          Fungsi invers f ^-1 : B → A adalah sebuah fungsi dimana untuk setiap b ∊  B mempunyai bayangan tunggal dalam himpunan A. Dengan demikian hanya fungsi satu-satu yang memiliki fungsi invers.

          Contoh :

          f : A → B bukan fungsi satu-satu, sehingga tidak memiliki fungsi invers f ^-1 .

                                   

          f : A →  B adalah fungsi satu-satu, sehingga memiliki fungsi invers f ^-1 : B →  A.

               

5. Komposisi Fungsi

Komposisi dari fungsi f dan g dinyatakan oleh (g_of).

          Jika f : A →  B dan g : B →  C, maka :

          (g_of) : A →  C

          (g_of) (a) : g (f (a))     

          Contoh :

          Diberikan fungsi f(x) = x -1 dan g(x) = x² + 1. Tentukan f_og dan g_of.

          Penyelesaian :

(i)                 (f_og)(x) = f(g(x)) = f(x²+1) = x²+1 – 1 = x²

(ii)               (g_of)(x) = g(f(x)) = g(x – 1) = (x – 1)² + 1 = x² + 2.

DAFTAR PUSTAKA 

Drs. Jong Jiak Siang, M. (2006). Matematika Diskrit dan Aplikasinya pada Ilmu Komputer. Yogyakarta: C.V ANDI OFFSET.

Wibisono, S. (2008). MATEMATIKA DISKRIT. Yogyakarta: GRAHA ILMU.

"Operasi Perulangan"

Assalamualaikum Warohmatullohi Wabarokatuh...

C++ adalah bahasa pemrograman komputer yang di buat oleh Bjarne Stroustrup, yang merupakan perkembangan dari bahasa C dikembangkan di Bong Labs (Dennis Ritchie) pada awal tahun 1970-an, Bahasa itu diturunkan dari bahasa sebelumnya, yaitu B.

Pada kesempatan kali ini, saya akan berbagi ilmu tentang "Operasi Perulangan" dalam kasus sehari hari menggunakan bahasa C++.

1.    Pengertian Operasi Perulangan

      Dalam suatu kasus banyak terdapat data yang sangat banyak dan hampir sama bentuknya. Dalam        hal ini diperlukan kode baru yang bertujuan agar memudahkan kita dalam kasus itu karena tidak          perlu banyak menuliskan program yang sama.

2.    Bentuk Umum Struktur Penulisan

a.    Perulangan menggunakan "for"
      for ( inisialisasi; syarat pengulangan; pengubah nilai pencacah )
     {
        pernyataan / perintah;
        pernyataan / perintah;
        pernyataan / perintah;

 }

b. Perulangan menggunakan "goto"

     ulang:

cout<<"Menu Yang Ada Dirumah Makan Cucu :\n";

cout<<"A.Hemat 1\n";

cout<<"B.Hemat 2\n\n";

cout<<"Masukkan Pilihan Layanan [A/B] : ";      cin>>kode1;

switch (kode1)

{

   case 'A':

   case 'a':

        cout<<"Paket Hemat 1 Harus Dipesan Minimal 3 Orang\n";

        cout<<"Makanan Yang Disediakan Adalah : Nasi, Dada Ayam, dan Es Teh\n";

        cout<<"Masukkan Banyak Pemesan : ";         cin>>A;

        if (A>=3)

        {

            Nama= "Nasi, Dada Ayam, dan Es Teh";

            Harga=20000*A;

            cout<<"Harganya Adalah Rp."<<Harga<<",-\n";

         }

         else if (A<3)         

         {

            cout<<"Anda Tidak Dapat Memilih Paket Ini, Silahkan Ulangi Pilihan Anda\n\n";

                goto ulang;

         }

3.    Listing Program   

4. Hasil Running  

Sumber :

Frieyadie, S. (2007). Borland C++. Jakarta: DIKTAT KULIAH PEMROGRAMAN KOMPUTER.

http://elektro.um.ac.id/wp-content/uploads/2016/04/Dasar-Pemrograman-Modul-1-Pengenalan-Pemrograman.pdf

"Operasi Penyeleksian Kondisi"

Assalamualaikum Warohmatullohi Wabarokatuh...

C++ adalah bahasa pemrograman komputer yang di buat oleh Bjarne Stroustrup, yang merupakan perkembangan dari bahasa C dikembangkan di Bong Labs (Dennis Ritchie) pada awal tahun 1970-an, Bahasa itu diturunkan dari bahasa sebelumnya, yaitu B.

Pada kesempatan kali ini, saya akan berbagi ilmu tentang "Operasi Penyeleksian Kondisi" dalam kasus sehari hari menggunakan bahasa C++.

1.    Pengertian Operasi Penyeleksian Kondisi

     Adalah Pernyataan Percabangan digunakan untuk memecahkan persoalan untuk mengambil suatu       keputusan diantara sekian pernyataan yang ada.

2.    Bentuk Umum Struktur Penulisan

a.    Penyeleksian Kondisi menggunakan "if else"

if (syarat)

{

… perintah;

… perintah;

}

else if (syarat)

{

… perintah;

… perintah;

}

else

{

… perintah;

… perintah;

}

b. Penyeleksian kondisi menggunakan "switch case"

switch (ekspresi integer atau karakter )

{

case konstanta-1 :

… perintah;

… perintah;

break;

case konstanta-2 :

… perintah;

… perintah;

break;

……

……

default :

… perintah;

… perintah;

}

3.    Listing Program

     a. Listing Program Menggunakan "if else"

     b. Listing Program Menggunakan "switch case"

4. Hasil Running

    a. Hasil Running "if else"

    b. Hasil Running "switch case"

Sumber :

Frieyadie, S. (2007). Borland C++. Jakarta: DIKTAT KULIAH PEMROGRAMAN KOMPUTER.

http://elektro.um.ac.id/wp-content/uploads/2016/04/Dasar-Pemrograman-Modul-1-Pengenalan-Pemrograman.pdf